BYSEX21C08SA
You can use the PMT function to calculate the amount to be paid each month, either to pay off a loan or to reach a certain savings goal.
Correct!
Review the section "PMT Function."
This image shows how to determine the remaining balance of a $20,000 loan after five years with a monthly payment of $250 and a constant interest rate of 4.5%.

Correct!
Review the section "Financial Function Arguments."
Judy wants to see how much interest she will pay on a loan if she takes 5, 7, or 10 years to pay it off, so she uses Goal Seek to calculate the varying interest amounts.
Correct!
Review the section "Using Data Tables."
For a one-variable data table, the formula must be located either at the top or right of the table, and for a two-variable data table, it must be in the upper-right cell.
Correct!
Review the section "Using Data Tables."
For each scenario you create, you must indicate a scenario name, the changing cells, and the values for each of the changing cells.
Correct!
Review the section "Scenario Manager."
You can use a Goal Seek like this to determine how much you can afford to spend on a car, assuming a monthly payment of $250 and a fixed interest rate and term.

Correct!
Review the section "Goal Seek."
You just received a big promotion at work and are shopping for a new luxury car. To calculate your monthly payment based on the inputs shown, the formula in cell B4 would be:

Correct!
Review the section "PMT Function."
Barb wants to save $500,000 for retirement and can put away $500/month into an account that earns 3.5% interest. Which function should Barb use to determine when she can retire?
Correct!
Review the section "NPER Function."
You are creating a one-variable data table to see how much more interest you will pay if you increase the length of your car loan. The formula in cell E5 is =B8*B7-B5. What variable do you use for the input cell?
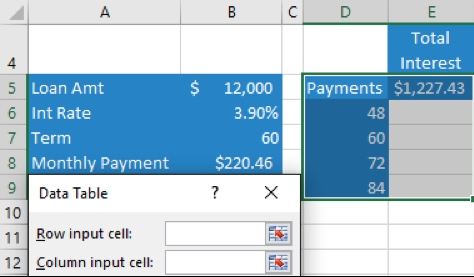
Correct!
Review the section "Using Data Tables."
You are buying a new home theater system and have narrowed your search to two options. You want to compare monthly payments and total interest over the life of the loan for the two systems, which have different prices, terms, and interest rates. Which tool do you use?
Correct!
Review the section "Scenario Manager."
The Scenario Manager allows you to substitute multiple values into one or more formulas. How many variables can you have in a scenario?
Correct!
Review the section "Scenario Manager."
Cell B7 contains the formula =PMT(B5/12,B6,-B4) and all other cells contain constant values. Which cell(s) can be used as the set cell in a Goal Seek?

Correct!
Review the section "Goal Seek."